Hur man hittar området av en likriktad triangel

Matematik, och geometri i synnerhet, enligtpolls av skolbarn, en av de mest oförlösta lektionerna, och allt för att de får dig att lära dig ett stort antal formler som i livet har 90% av nuvarande vuxna inte hittat praktisk tillämpning. Men i en minut läser vi formler, löser problem, gör ekvationer inte för att de kan vara användbara för oss i livet, men för att det utvecklar tänkande och logik. Även de antika grekiska sagesna sade att det mänskliga intellektet kan mätas med kunskap om matematiska vetenskaper. Och sedan du bestämde dig för att bekanta dig med användningen av formlerna för en ensam trekant - tar vi oss till hands och läser hela artikeln.
Innan du börjar svara på frågan hur du hittarområdet av en likvärdig triangel och gå till den praktiska delen av artikeln, där formler och beräkningar ges, låt oss beteckna själva begreppet för oss själva. En likriktad triangel är en triangel där två av de tre sidorna är lika långa, kallade sidosidor. När det gäller en vanlig triangel, där alla sidor är lika, betraktas det också somoseller, men vice versa, när en likriktad triangel anses korrekt - är felaktig.
Sidorna av triangeln ska betecknas, vi kommer att göra det på detta sätt, som visas på bilden nedan, där: a - sidor, b-bas och h-höjd.
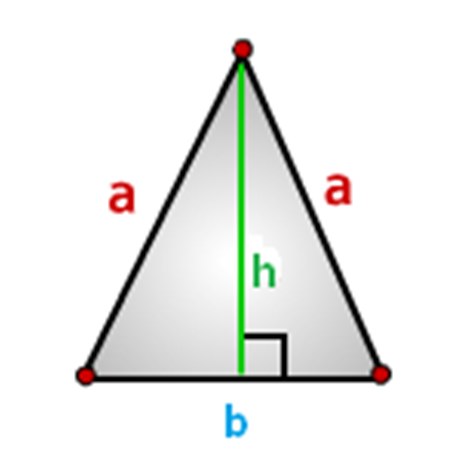
Hur man beräknar området med en likriktad triangel, formler.
När vi har noterat höjd, sidor och vinklar kan vi börja lösa problemet.
Till att börja med bestämmer vi vad vi vet.
Om höjden och botten - då den klassiska formeln (* - multiplikationstecken):
S = ½ * b * h
Låt oss ersätta, till exempel, siffrorna där: h = 16, b = 18, vi får följande:
S = ½ * 18 * 16 = 9 * 16 = 144;
Arean av en likriktad triangel är S = 144 cm2
Det finns andra formler som hjälper osshur man känner till området av en likriktad triangel. En sådan formel är Herons metod. Låt oss inte skriva en komplex formel, vi tar på grund av en förkortad:
S = ¼ b √4 * a2-b2
Det är uppenbart att b är grunden, och - lika sidor. Formeln är lämplig om h-höjden är okänd.
Byt värdena, låt a = 6, b = 3, vi får följande:
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
Du kan använda för att beräkna området lika med sidorna av triangeln och vinkeln mellan sidorna:
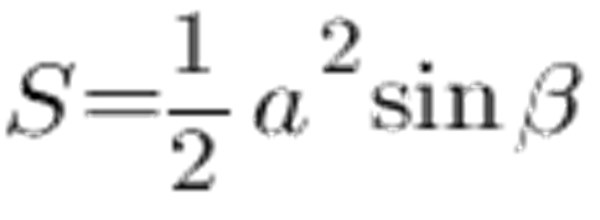
Enligt sinusbordet är vinkeln vid 45 ° lika med 0.7071, sidan a och låt den vara 6 cm, vi får följande:
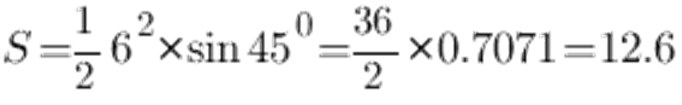
Som ett resultat är arean av en likriktad triangel 12,6 cm2.
Det finns också sätt att beräkna området, inklusiveinklusive i fråga om en likvärdig triangel, men de är ganska komplicerade och gäller inte för "elementära" beräkningar, såsom de som anges ovan, i begreppet komplex matematik. Och det är inte värt att prata om saker som även lärare med erfarenhet inte förstår.
Så, du kan andas lättnad suck på dettaen liten kurs av geometri för att hitta området av en isosceles triangel anses vara fullständig och den kunskap som erhålls som en följd av att läsa artikeln lärs av "fem".














